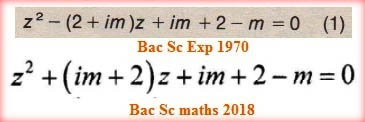العماري سيموح
مقارنة الاختبار الوطني للرياضيات ع رياضية 2018 مع ع تجريبية 1970
الإثنين 02 يوليو 2018 | 20:32